Iterative Smoothing of Field Data in Spherical Meshes

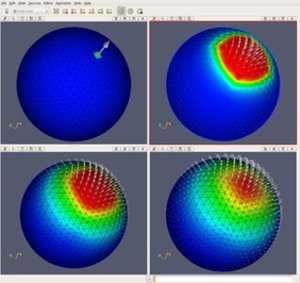
This document describes a contribution to the Insight Toolkit intended to smooth the values of Field data associated with the nodes of a Spherical Mesh. The Mesh Smoothing filters contributed here do not modify the geometry or the topology of the Mesh. They act only upon the pixel data values associated with the nodes. Two filters are presented, one that smooths scalar field data, and a second one that smooths vector field data. This paper is accompanied with the source code, input data, parameters and output data that we used for validating the algorithm described in this paper. This adheres to the fundamental principle that scientific publications must facilitate reproducibility of the reported results.